viernes, 11 de octubre de 2013
lunes, 9 de septiembre de 2013
Geometría Analítica
Definición de Geometría Analítica:
Rama de las matemáticas en la cual se afirma que a cada lugar geométrico le corresponde una ecuación y viceversa.
Concepto de Pendiente:
pendiente de la ecuación de una recta como caso particular de la tangente a una curva, en cuyo caso representa la derivada de la función en el punto considerado, y es un parámetro relevante.
René Descartes
(La Haye, Francia, 1596 - Estocolmo, Suecia, 1650)
Filósofo y matemático francés. René Descartes se educó en el colegio
jesuita de La Flèche (1604-1612), donde gozó de un cierto trato de favor
en atención a su delicada salud.
Obtuvo el título
de bachiller y de licenciado en derecho por la facultad de Poitiers
(1616), y a los veintidós años partió hacia los Países Bajos, donde
sirvió como soldado en el ejército de Mauricio de Nassau. En 1619 se
enroló en las filas del duque de Baviera; el 10 de noviembre, en el
curso de tres sueños sucesivos, René Descartes experimentó la famosa
«revelación» que lo condujo a la elaboración de su método.
Tras
renunciar a la vida militar, Descartes viajó por Alemania y los Países
Bajos y regresó a Francia en 1622, para vender sus posesiones y
asegurarse así una vida independiente; pasó una temporada en Italia
(1623-1625) y se afincó luego en París, donde se relacionó con la
mayoría de científicos de la época. En 1628 decidió instalarse en los
Países Bajos lugar que consideró más favorable para cumplir los
objetivos filosóficos y científicos que se había fijado, y residió allí
hasta 1649.
Los cinco primeros años los dedicó
principalmente a elaborar su propio sistema del mundo y su concepción
del hombre y del cuerpo humano, que estaba a punto de completar en 1633
cuando, al tener noticia de la condena de Galileo, renunció a la
publicación de su obra, que tendría lugar póstumamente.
En 1637 apareció su famoso Discurso del método,
presentado como prólogo a tres ensayos científicos. Descartes proponía
una duda metódica, que sometiese a juicio todos los conocimientos de la
época, aunque, a diferencia de los escépticos, la suya era una duda
orientada a la búsqueda de principios últimos sobre los cuales cimentar
sólidamente el saber.
Este principio lo halló en la
existencia de la propia conciencia que duda, en su famosa formulación
«pienso, luego existo». Sobre la base de esta primera evidencia, pudo
desandar en parte el camino de su escepticismo, hallando en Dios el
garante último de la verdad de las evidencias de la razón, que se
manifiestan como ideas «claras y distintas».
El método cartesiano, que Descartes propuso para todas
las ciencias y disciplinas, consiste en descomponer los problemas
complejos en partes progresivamente más sencillas hasta hallar sus
elementos básicos, las ideas simples, que se presentan a la razón de un
modo evidente, y proceder a partir de ellas, por síntesis, a reconstruir
todo el complejo, exigiendo a cada nueva relación establecida entre
ideas simples la misma evidencia de éstas.
Los
ensayos científicos que seguían, ofrecían un compendio de sus teorías
físicas, entre las que destaca su formulación de la ley de inercia y una
especificación de su método para las matemáticas. Los fundamentos de su
física mecanicista, que hacía de la extensión la principal propiedad de
los cuerpos materiales, los situó en la metafísica que expuso en 1641,
donde enunció así mismo su demostración de la existencia y la perfección
de Dios y de la inmortalidad del alma. El mecanicismo radical de las
teorías físicas de Descartes, sin embargo, determinó que fuesen
superadas más adelante.
Pronto su filosofía empezó a
ser conocida y comenzó a hacerse famoso, lo cual le acarreó amenazas de
persecución religiosa por parte de algunas autoridades académicas y
eclesiásticas, tanto en los Países Bajos como en Francia. En 1649 aceptó
la invitación de la reina Cristina de Suecia y se desplazó a Estocolmo,
donde murió cinco meses después de su llegada a consecuencia de una
neumonía.
Descartes es considerado como el iniciador
de la filosofía racionalista moderna por su planteamiento y resolución
del problema de hallar un fundamento del conocimiento que garantice la
certeza de éste, y como el filósofo que supone el punto de ruptura
definitivo con la escolástica.

François Vieta o Viète
(Fontenay-le-Comte, Francia, 1540 - París, 1603) Matemático francés. Fue
miembro del Parlamento de Bretaña (1573-1582) y después consejero
privado de las cortes de Enrique III y de Enrique IV.
Conocedor de la obra del matemático griego Diofanto de Alejandría y de los recientes estudios del italiano Gerolamo Cardano, François Viète estableció las reglas para la extracción de raíces y dio a la trigonometría su forma definitiva en Canon mathematicus (1570). Se dedicó asimismo al estudio de los fundamentos del álgebra, con la publicación, en 1591, de In artem analyticam isagoge,
en el cual introdujo un sistema de notación que hacía uso de letras en
las fórmulas algebraicas. Se ocupó finalmente de diversas cuestiones
geométricas, como la trigonometría plana y esférica.

Circunferencia
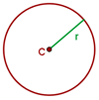
La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.
Elementos de la circunferencia
Centro de la circunferencia
El centro es el punto del que equidistan todos los puntos de la circunferencia.
Radio de la circunferencia
El radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Cuerda

La cuerda es un segmento que une dos puntos de la circunferencia.
Diámetro
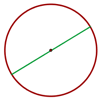
El diámetro es una cuerda que pasa por el centro de la circunferencia.
El diámetro mide el doble del radio.
Arco
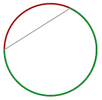
Un arco es cada una de las partes en que una cuerda divide a la circunferencia.
Se suele asociar a cada cuerda el menor arco que delimita.
Semicircunferencia
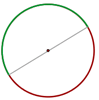
Una semicircunferencia es cada uno de los arcos iguales que abarca un diámetro.
Longitud de una circunferencia
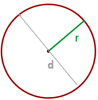
La longitud de una circunferencia es igual a pi por el diámetro.
La longitud de una circunferencia es igual a 2 pi por el radio.
Ángulos en la circunferencia
Ángulo central

El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
Ángulo inscrito

El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
Mide la mitad del arco que abarca.
Ángulo semi-inscrito

El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.
Ángulo interior

Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
Ángulo exterior
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:



Mide la mitad de la diferencia entre las medidas de los arcos que abarcan sus lados sobre la circunferencia.
Posiciones relativas de un punto respecto a una circunferencia
Interior
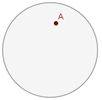
La distancia del punto al centro es menor que el radio.
Punto sobre la circunferencia.
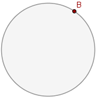
El punto pertenece a la circunferencia.
Punto exterior a la circunferencia

La distancia del punto al centro es mayor que el radio.
Posiciones relativas de una recta y una circunferencia
Recta secante
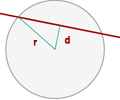
La recta corta a la circunferencia en dos puntos.
Recta tangente
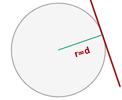
La recta corta a la circunferencia en un punto.
Recta exterior
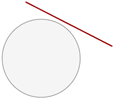
No tiene ningún punto de corte con la circunferencia.
Posiciones relativas de dos circunferencias
Ningún punto en común
Exteriores
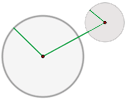
La distancia entre los centros es mayor que la suma de las radios.
Interiores
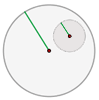
La distancia entre los centros es menor que la diferencia de los radios.
Concéntricas
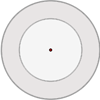
Los centros coinciden.
Un punto común
Tangentes exteriores
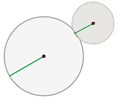
La distancia entre los centros es igual a la suma de los radios.
Tangentes interiores

La distancia entre los centros es igual a la diferencia de los radios.
Dos puntos en común
Secantes

La distancia entre los centros es mayor que la diferencia de los radios.
Suscribirse a:
Entradas (Atom)